Centered polygonal number

The centered polygonal numbers are a class of series of figurate numbers, each formed by a central dot, surrounded by polygonal layers with a constant number of sides. Each side of a polygonal layer contains one dot more than a side in the previous layer, so starting from the second polygonal layer each layer of a centered k-gonal number contains k more points than the previous layer.

Examples

Each element in the sequence is a multiple of the previous triangular number plus 1. This can be formalized by the equation ${\frac {ax(x+1)}{2}}+1$ where a is the number of sides of the polygon, and x is the sequence number, starting with zero for the initial 1. For example, the centered square numbers are four times the triangular numbers plus 1, or equivalently ${\frac {4x(x+1)}{2}}+1$ .

These series consist of the

centered triangular numbers 1, 4, 10, 19, 31, 46, 64, 85, 109, 136, 166, 199, ... (OEIS: A005448)
centered square numbers 1, 5, 13, 25, 41, 61, 85, 113, 145, 181, 221, 265, ... (OEIS: A001844)
centered pentagonal numbers 1, 6, 16, 31, 51, 76, 106, 141, 181, 226, 276, 331, ... (OEIS: A005891)
centered hexagonal numbers 1, 7, 19, 37, 61, 91, 127, 169, 217, 271, 331, 397, ... (OEIS: A003215), which are exactly the difference of consecutive cubes, i.e. x³ − (x − 1)³
centered heptagonal numbers 1, 8, 22, 43, 71, 106, 148, 197, 253, 316, 386, 463, ... (OEIS: A069099)
centered octagonal numbers 1, 9, 25, 49, 81, 121, 169, 225, 289, 361, 441, 529, ... (OEIS: A016754), which are exactly the odd squares
centered nonagonal numbers 1, 10, 28, 55, 91, 136, 190, 253, 325, 406, 496, 595, ... (OEIS: A060544), which include all even perfect numbers except 6
centered decagonal numbers 1, 11, 31, 61, 101, 151, 211, 281, 361, 451, 551, 661, ... (OEIS: A062786)
centered hendecagonal numbers 1, 12, 34, 67, 111, 166, 232, 309, 397, 496, 606, 727, ... (OEIS: A069125)
centered dodecagonal numbers 1, 13, 37, 73, 121, 181, 253, 337, 433, 541, 661, 793, ... (OEIS: A003154), which are also the star numbers

and so on.

The following diagrams show a few examples of centered polygonal numbers and their geometric construction. Compare these diagrams with the diagrams in Polygonal number.

centered triangular number	centered square number	centered pentagonal number	centered hexagonal number

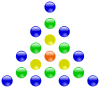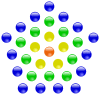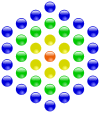Centered square numbers

1		5		13		25

Centered hexagonal numbers

1		7		19		37

Formula

As can be seen in the above diagrams, the nth centered k-gonal number can be obtained by placing k copies of the (n−1)th triangular number around a central point; therefore, the nth centered k-gonal number can be mathematically represented by

C_{{k,n}}={\frac {kn}{2}}(n-1)+1.

The difference of the n-th and the (n+1)-th consecutive centered k-gonal numbers is k(2n+1).

The n-th centered k-gonal number is equal to the n-th regular k-gonal number plus (n-1)².

Just as is the case with regular polygonal numbers, the first centered k-gonal number is 1. Thus, for any k, 1 is both k-gonal and centered k-gonal. The next number to be both k-gonal and centered k-gonal can be found using the formula:

{\frac {k^{2}}{2}}(k-1)+1

which tells us that 10 is both triangular and centered triangular, 25 is both square and centered square, etc.

Whereas a prime number p cannot be a polygonal number (except the trivial case, i.e. each p is the second p-gonal number), many centered polygonal numbers are primes. In fact, if k ≥ 3, k ≠ 8, k ≠ 9, then there are infinitely many centered k-gonal numbers which are primes (assuming the Bunyakovsky conjecture). (Since all centered octagonal numbers are also square numbers, and all centered nonagonal numbers are also triangular numbers (and not equal to 3), thus both of them cannot be prime numbers)

Sum of Reciprocals

The sum of reciprocals for the centered k-gonal numbers is^[1]

{\frac {2\pi }{k{\sqrt {1-{\frac {8}{k}}}}}}\tan \left({\frac {\pi }{2}}{\sqrt {1-{\frac {8}{k}}}}\right)

, if k ≠ 8

{\frac {\pi ^{2}}{8}}

, if k = 8

References

^ centered polygonal numbers in OEIS wiki, content "Table of related formulae and values"

Neil Sloane & Simon Plouffe (1995). The Encyclopedia of Integer Sequences. San Diego: Academic Press.: Fig. M3826
Weisstein, Eric W. "Centered polygonal number". MathWorld.
F. Tapson (1999). The Oxford Mathematics Study Dictionary (2nd ed.). Oxford University Press. pp. 88–89. ISBN 0-19-914-567-9.

[1] tered polygonal numbers in OEIS wiki, content "Table of related formulae and values"

[1]