Centered heptagonal number

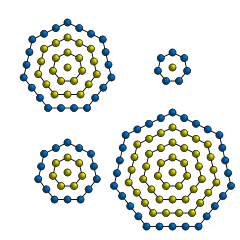
A centered heptagonal number is a centered figurate number that represents a heptagon with a dot in the center and all other dots surrounding the center dot in successive heptagonal layers. The centered heptagonal number for n is given by the formula

.

This can also be calculated by multiplying the triangular number for (n – 1) by 7, then adding 1.

The first few centered heptagonal numbers are

1, 8, 22, 43, 71, 106, 148, 197, 253, 316, 386, 463, 547, 638, 736, 841, 953 (sequence A069099 in the OEIS)

Centered heptagonal numbers alternate parity in the pattern odd-even-even-odd.

Centered heptagonal prime

A centered heptagonal prime is a centered heptagonal number that is prime. The first few centered heptagonal primes are

43, 71, 197, 463, 547, 953, 1471, 1933, 2647, 2843, 3697, ... (sequence A144974 in the OEIS)

and centered heptagonal twin prime numbers are

43, 71, 197, 463, 1933, 5741, 8233, 9283, 11173, 14561, 34651, ... (sequence A144975 in the OEIS).

See also

• Regular heptagonal number.