Zassenhaus lemma

Hasse diagram of the Zassenhaus "butterfly" lemma – smaller subgroups are towards the top of the diagram

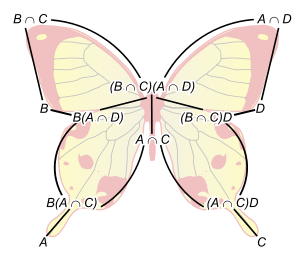
In mathematics, the butterfly lemma or Zassenhaus lemma, named after Hans Zassenhaus, is a technical result on the lattice of subgroups of a group or the lattice of submodules of a module, or more generally for any modular lattice.^[1]

Lemma. Suppose

G

is a group with subgroups

A

and

C

. Suppose

B\triangleleft A

and

D\triangleleft C

are normal subgroups. Then there is an isomorphism of quotient groups:

{\frac {(A\cap C)B}{(A\cap D)B}}\cong {\frac {(A\cap C)D}{(B\cap C)D}}.

This can be generalized to the case of a group with operators $(G, \Omega)$ with stable subgroups $A$ and $C$ , the above statement being the case of $\Omega =G$ acting on itself by conjugation.

Zassenhaus proved this lemma specifically to give the most direct proof of the Schreier refinement theorem. The 'butterfly' becomes apparent when trying to draw the Hasse diagram of the various groups involved.

Zassenhaus' lemma for groups can be derived from a more general result known as Goursat's theorem stated in a Goursat variety (of which groups are an instance); however the group-specific modular law also needs to be used in the derivation.^[2]

References

^ Pierce, R.S. (1982). Associative algebras. Springer. p. 27, exercise 1. ISBN 0-387-90693-2.
^ J. Lambek (1996). "The Butterfly and the Serpent". In Aldo Ursini; Paulo Agliano (eds.). Logic and Algebra. CRC Press. pp. 161–180. ISBN 978-0-8247-9606-8.

Resources

Goodearl, K. R.; Warfield, Robert B. (1989), An introduction to noncommutative noetherian rings, Cambridge University Press, pp. 51, 62, ISBN 978-0-521-36925-1.
Lang, Serge, Algebra, Graduate Texts in Mathematics (Revised 3rd ed.), Springer-Verlag, pp. 20–21, ISBN 978-0-387-95385-4.
Carl Clifton Faith, Nguyen Viet Dung, Barbara Osofsky (2009) Rings, Modules and Representations. p. 6. AMS Bookstore, ISBN 0-8218-4370-2
Hans Zassenhaus (1934) "Zum Satz von Jordan-Hölder-Schreier", Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg 10:106–8.
Hans Zassenhaus (1958) Theory of Groups, second English edition, Lemma on Four Elements, p 74, Chelsea Publishing.

External links

Zassenhaus Lemma and proof at https://web.archive.org/web/20080604141650/http://www.artofproblemsolving.com:80/Wiki/index.php/Zassenhaus%27s_Lemma

[1] Pierce, R.S. (1982). Associative algebras. Springer. p. 27, exercise 1. ISBN 0-387-90693-2.

[2] J. Lambek (1996). "The Butterfly and the Serpent". In Aldo Ursini; Paulo Agliano (eds.). Logic and Algebra. CRC Press. pp. 161–180. ISBN 978-0-8247-9606-8.

[1]

[2]