Van Aubel's theorem

The theorem can be applied to a complex (self-intersecting) quadrilateral.

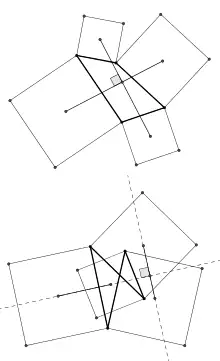
In plane geometry, Van Aubel's theorem describes a relationship between squares constructed on the sides of a quadrilateral. Starting with a given convex quadrilateral, construct a square, external to the quadrilateral, on each side. Van Aubel's theorem states that the two line segments between the centers of opposite squares are of equal lengths and are at right angles to one another. Another way of saying the same thing is that the center points of the four squares form the vertices of an equidiagonal orthodiagonal quadrilateral. The theorem is named after H. H. van Aubel, who published it in 1878.^[1]

The theorem holds true also for re-entrant quadrilaterals,^[2] and when the squares are constructed internal to the given quadrilateral.^[3] For complex (self-intersecting) quadrilaterals, the external and internal constructions for the squares are not definable. In this case, the theorem holds true when the constructions are carried out in the more general way:^[3]

• follow the quadrilateral vertexes in a sequential direction and construct each square on the right hand side of each side of the given quadrilateral.
• Follow the quadrilateral vertexes in the same sequential direction and construct each square on the left hand side of each side of the given quadrilateral.

The segments connecting the centers of the squares constructed externally (or internally) to the quadrilateral over two opposite sides have been referred to as Van Aubel segments. The points of intersection of two equal and orthogonal Van Aubel segments (produced when necessary) have been referred to as Van Aubel points:^[3] first or outer Van Aubel point for the external construction, second or inner Van Aubel point for the internal one.

A few extensions of the theorem, considering similar rectangles, similar rhombi and similar parallelograms constructed on the sides of the given quadrilateral, have been published on the The Mathematical Gazette.^{[4] [5]}

See also

• Petr–Douglas–Neumann theorem
• Thébault's theorem
• Napoleon's theorem
• Napoleon points
• Bottema's theorem

References

External links

• Weisstein, Eric W. "van Aubel's Theorem". MathWorld.
• Van Aubel's Theorem for Quadrilaterals and Van Aubel's Theorem for Triangles by Jay Warendorff, The Wolfram Demonstrations Project.
• The Beautiful Geometric Theorem of Van Aubel by Yutaka Nishiyama, International Journal of Pure and Applied Mathematics.
• Interactive applet by Tim Brzezinski showing Van Aubel's Theorem made using GeoGebra.
• Some generalizations of Van Aubel's theorem to similar quadrilaterals at Dynamic Geometry Sketches, interactive geometry sketches.
• QG-2P6: Outer and Inner Van Aubel Points by Chris Van Tienhoven at Encyclopedia of Quadri-Figures (EQF).