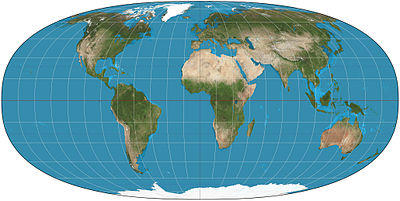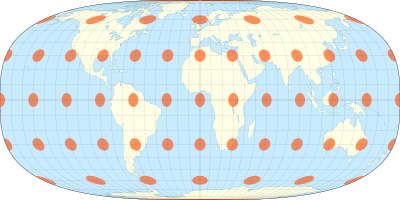
The Tobler hyperelliptical projection is a family of equal-area pseudocylindrical projections that may be used for world maps. Waldo R. Tobler introduced the construction in 1973 as the hyperelliptical projection, now usually known as the Tobler hyperelliptical projection.[1]
Overview
As with any pseudocylindrical projection, in the projection’s normal aspect,[2] the parallels of latitude are parallel, straight lines. Their spacing is calculated to provide the equal-area property. The projection blends the cylindrical equal-area projection with meridians of longitude that follow a particular kind of curve known as superellipses[3] or Lamé curves or sometimes as hyperellipses. The curve is described by xk + yk = γk. The relative weight of the cylindrical equal-area projection is given as α, ranging from all cylindrical equal-area with α = 1 to all hyperellipses with α = 0.
When α = 0 and k = 1 the projection degenerates to the Collignon projection; when α = 0, k = 2, and γ ≈ 1.2731 the projection becomes the Mollweide projection.[4] Tobler favored the parameterization shown with the top illustration; that is, α = 0, k = 2.5, and γ = 1.183136.
See also
- List of map projections
References
- ^ Snyder, John P. (1993). Flattening the Earth: 2000 Years of Map Projections. Chicago: University of Chicago Press. p. 220.
- ^ The Tobler Hyperelliptical Projection on the Center for Spatially Integrated Social Science's site
- ^ "Superellipse" in MathWorld encyclopedia
- ^ Tobler, Waldo (1973). "The hyperelliptical and other new pseudocylindrical equal area map projections". Journal of Geophysical Research. 78 (11): 1753–1759. Bibcode:1973JGR....78.1753T. CiteSeerX 10.1.1.495.6424. doi:10.1029/JB078i011p01753.