Mercator series

Polynomial approximation to logarithm with n=1, 2, 3, and 10 in the interval (0,2).

In mathematics, the Mercator series or Newton–Mercator series is the Taylor series for the natural logarithm:

\ln(1+x)=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-{\frac {x^{4}}{4}}+\cdots

In summation notation,

\ln(1+x)=\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}x^{n}.

The series converges to the natural logarithm (shifted by 1) whenever $-1<x\leq 1$ .

History

The series was discovered independently by Johannes Hudde ^[1] and Isaac Newton. It was first published by Nicholas Mercator, in his 1668 treatise Logarithmotechnia.

Derivation

The series can be obtained from Taylor's theorem, by inductively computing the n^th derivative of $\ln(x)$ at $x=1$ , starting with

{\frac {d}{dx}}\ln(x)={\frac {1}{x}}.

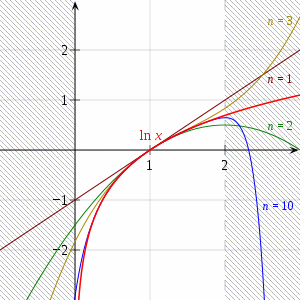
Alternatively, one can start with the finite geometric series ( $t\neq -1$ )

1-t+t^{2}-\cdots +(-t)^{n-1}={\frac {1-(-t)^{n}}{1+t}}

which gives

{\frac {1}{1+t}}=1-t+t^{2}-\cdots +(-t)^{n-1}+{\frac {(-t)^{n}}{1+t}}.

It follows that

\int _{0}^{x}{\frac {dt}{1+t}}=\int _{0}^{x}\left(1-t+t^{2}-\cdots +(-t)^{n-1}+{\frac {(-t)^{n}}{1+t}}\right)\ dt

and by termwise integration,

\ln(1+x)=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-\cdots +(-1)^{n-1}{\frac {x^{n}}{n}}+(-1)^{n}\int _{0}^{x}{\frac {t^{n}}{1+t}}\ dt.

If $-1<x\leq 1$ , the remainder term tends to 0 as $n\to \infty$ .

This expression may be integrated iteratively k more times to yield

-xA_{k}(x)+B_{k}(x)\ln(1+x)=\sum _{n=1}^{\infty }(-1)^{n-1}{\frac {x^{n+k}}{n(n+1)\cdots (n+k)}},

where

A_{k}(x)={\frac {1}{k!}}\sum _{m=0}^{k}{k \choose m}x^{m}\sum _{l=1}^{k-m}{\frac {(-x)^{l-1}}{l}}

and

B_{k}(x)={\frac {1}{k!}}(1+x)^{k}

are polynomials in x.^[2]

Special cases

Setting $x=1$ in the Mercator series yields the alternating harmonic series

\sum _{k=1}^{\infty }{\frac {(-1)^{k+1}}{k}}=\ln(2).

Complex series

The complex power series

\sum _{n=1}^{\infty }{\frac {z^{n}}{n}}=z+{\frac {z^{2}}{2}}+{\frac {z^{3}}{3}}+{\frac {z^{4}}{4}}+\cdots

is the Taylor series for $-\log(1-z)$ , where log denotes the principal branch of the complex logarithm. This series converges precisely for all complex number $|z|\leq 1,z\neq 1$ . In fact, as seen by the ratio test, it has radius of convergence equal to 1, therefore converges absolutely on every disk B(0, r) with radius r < 1. Moreover, it converges uniformly on every nibbled disk $\scriptstyle \overline{B(0,1)}\setminus B(1,\delta)$ , with δ > 0. This follows at once from the algebraic identity:

(1-z)\sum _{n=1}^{m}{\frac {z^{n}}{n}}=z-\sum _{n=2}^{m}{\frac {z^{n}}{n(n-1)}}-{\frac {z^{m+1}}{m}},

observing that the right-hand side is uniformly convergent on the whole closed unit disk.

References

^ https://dspace.library.uu.nl/handle/1874/251283
^ Medina, Luis A.; Moll, Victor H.; Rowland, Eric S. (2009). "Iterated primitives of logarithmic powers". International Journal of Number Theory. 7: 623–634. arXiv:0911.1325. doi:10.1142/S179304211100423X.

Weisstein, Eric W. "Mercator Series". MathWorld.
Anton von Braunmühl (1903) Vorlesungen über Geschichte der Trigonometrie, Seite 134, via Internet Archive
Eriksson, Larsson & Wahde. Matematisk analys med tillämpningar, part 3. Gothenburg 2002. p. 10.
Some Contemporaries of Descartes, Fermat, Pascal and Huygens from A Short Account of the History of Mathematics (4th edition, 1908) by W. W. Rouse Ball

[1] ttps://dspace.library.uu.nl/handle/1874/251283

[2] Medina, Luis A.; Moll, Victor H.; Rowland, Eric S. (2009). "Iterated primitives of logarithmic powers". International Journal of Number Theory. 7: 623–634. arXiv:0911.1325. doi:10.1142/S179304211100423X.

[1]