Euler's theorem in geometry

Euler's theorem:

d=|IO|={\sqrt {R(R-2r)}}

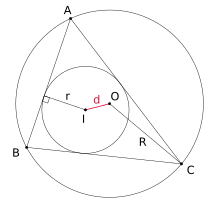
In geometry, Euler's theorem states that the distance d between the circumcentre and incentre of a triangle is given by^[1]^[2]

d^{2}=R(R-2r)

or equivalently

{\frac {1}{R-d}}+{\frac {1}{R+d}}={\frac {1}{r}},

where R and r denote the circumradius and inradius respectively (the radii of the circumscribed circle and inscribed circle respectively). The theorem is named for Leonhard Euler, who published it in 1765.^[3] However, the same result was published earlier by William Chapple in 1746.^[4]

From the theorem follows the Euler inequality:^[5]^[6]

R\geq 2r,

which holds with equality only in the equilateral case.^[7]^{:p. 198}

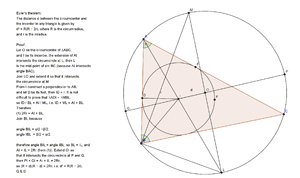
Proof

Proof of Euler's theorem in geometry

Letting O be the circumcentre of triangle ABC, and I be its incentre, the extension of AI intersects the circumcircle at L. Then L is the midpoint of arc BC. Join LO and extend it so that it intersects the circumcircle at M. From I construct a perpendicular to AB, and let D be its foot, so ID = r. It is not difficult to prove that triangle ADI is similar to triangle MBL, so ID / BL = AI / ML, i.e. ID × ML = AI × BL. Therefore 2Rr = AI × BL. Join BI. Because

∠ BIL = ∠ A / 2 + ∠ ABC / 2,

∠ IBL = ∠ ABC / 2 + ∠ CBL = ∠ ABC / 2 + ∠ A / 2,

we have ∠ BIL = ∠ IBL, so BL = IL, and AI × IL = 2Rr. Extend OI so that it intersects the circumcircle at P and Q; then PI × QI = AI × IL = 2Rr, so (R + d)(R − d) = 2Rr, i.e. d² = R(R − 2r).

Stronger version of the inequality

A stronger version^[7]^{:p. 198} is

{\frac {R}{r}}\geq {\frac {abc+a^{3}+b^{3}+c^{3}}{2abc}}\geq {\frac {a}{b}}+{\frac {b}{c}}+{\frac {c}{a}}-1\geq {\frac {2}{3}}\left({\frac {a}{b}}+{\frac {b}{c}}+{\frac {c}{a}}\right)\geq 2,

where a, b, c are the sidelengths of the triangle.

Euler's theorem for the escribed circle

If $r_{a}$ and $d_{a}$ denote respectively the radius of the escribed circle opposite to the vertex $A$ and the distance between its centre and the centre of the circumscribed circle, then $d_{a}^{2}=R(R+2r_{a})$ .

Euler's inequality in absolute geometry

Euler's inequality, in the form stating that, for all triangles inscribed in a given circle, the maximum of the radius of the inscribed circle is reached for the equilateral triangle and only for it, is valid in absolute geometry.^[8]

References

^ Johnson, Roger A. (2007) [1929], Advanced Euclidean Geometry, Dover Publ., p. 186.
^ Dunham, William (2007), The Genius of Euler: Reflections on his Life and Work, Spectrum Series, 2, Mathematical Association of America, p. 300, ISBN 9780883855584.
^ Gerry Leversha, G. C. Smith: Euler and Triangle Geometry. In: The Mathematical Gazette, Vol. 91, No. 522, Nov., 2007, S. 436–452 (JSTOR 40378417)
^ Chapple, William (1746), "An essay on the properties of triangles inscribed in and circumscribed about two given circles", Miscellanea Curiosa Mathematica, 4: 117–124. The formula for the distance is near the bottom of p.123.
^ Alsina, Claudi; Nelsen, Roger (2009), When Less is More: Visualizing Basic Inequalities, Dolciani Mathematical Expositions, 36, Mathematical Association of America, p. 56, ISBN 9780883853429.
^ Debnath, Lokenath (2010), The Legacy of Leonhard Euler: A Tricentennial Tribute, World Scientific, p. 124, ISBN 9781848165250.
^ ^a ^b Svrtan, Dragutin; Veljan, Darko (2012), "Non-Euclidean versions of some classical triangle inequalities", Forum Geometricorum, 12: 197–209.
^ Pambuccian, Victor; Schacht, Celia (2018), "Euler's inequality in absolute geoemtry", Journal of Geometry, 109 (Art. 8): 1–11, doi:10.1007/s00022-018-0414-6.

External links

Weisstein, Eric W. "Euler Triangle Formula". MathWorld.

[Johnson-1] Johnson, Roger A. (2007) [1929], Advanced Euclidean Geometry, Dover Publ., p. 186.

[2] Dunham, William (2007), The Genius of Euler: Reflections on his Life and Work, Spectrum Series, 2, Mathematical Association of America, p. 300, ISBN 9780883855584.

[3] Gerry Leversha, G. C. Smith: Euler and Triangle Geometry. In: The Mathematical Gazette, Vol. 91, No. 522, Nov., 2007, S. 436–452 (JSTOR 40378417)

[4] Chapple, William (1746), "An essay on the properties of triangles inscribed in and circumscribed about two given circles", Miscellanea Curiosa Mathematica, 4: 117–124. The formula for the distance is near the bottom of p.123.

[wlim-5] Alsina, Claudi; Nelsen, Roger (2009), When Less is More: Visualizing Basic Inequalities, Dolciani Mathematical Expositions, 36, Mathematical Association of America, p. 56, ISBN 9780883853429.

[lle-6] Debnath, Lokenath (2010), The Legacy of Leonhard Euler: A Tricentennial Tribute, World Scientific, p. 124, ISBN 9781848165250.

[SV-7] Svrtan, Dragutin; Veljan, Darko (2012), "Non-Euclidean versions of some classical triangle inequalities", Forum Geometricorum, 12: 197–209.

[PS-8] Pambuccian, Victor; Schacht, Celia (2018), "Euler's inequality in absolute geoemtry", Journal of Geometry, 109 (Art. 8): 1–11, doi:10.1007/s00022-018-0414-6.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]