Effective potential

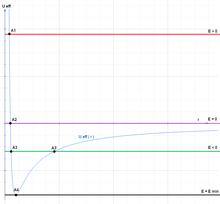
The effective potential (also known as effective potential energy) combines multiple, perhaps opposing, effects into a single potential. In its basic form, it is the sum of the 'opposing' centrifugal potential energy with the potential energy of a dynamical system. It may be used to determine the orbits of planets (both Newtonian and relativistic) and to perform semi-classical atomic calculations, and often allows problems to be reduced to fewer dimensions.

Definition

Effective potential. E> 0 hyperbola and A₁ is pericentrum, E = 0 parabola and A₂ is pericentrum, E <0 ellipse and A₃ is pericentrum A₃' is apocentrum, E=E_min circle and A₄ is radius. Points A₁, ..., A₄ are called turning points.

The basic form of potential $U_\text{eff}$ is defined as:

$U_{\text{eff}}(\mathbf {r} )={\frac {L^{2}}{2\mu r^{2}}}+U(\mathbf {r} )$ ,

where

L is the angular momentum

r is the distance between the two masses

μ is the reduced mass of the two bodies (approximately equal to the mass of the orbiting body if one mass is much larger than the other); and

U(r) is the general form of the potential.

The effective force, then, is the negative gradient of the effective potential:

${\begin{aligned}\mathbf {F} _{\text{eff}}&=-\nabla U_{\text{eff}}(\mathbf {r} )\\&={\frac {L^{2}}{\mu r^{3}}}{\hat {\mathbf {r} }}-\nabla U(\mathbf {r} )\end{aligned}}$ where ${\hat {\mathbf {r} }}$ denotes a unit vector in the radial direction.

Important properties

There are many useful features of the effective potential, such as

U_{{\text{eff}}}\leq E

.

To find the radius of a circular orbit, simply minimize the effective potential with respect to $r$ , or equivalently set the net force to zero and then solve for $r_{0}$ :

\frac{d U_\text{eff}}{dr} = 0

After solving for $r_{0}$ , plug this back into $U_\text{eff}$ to find the maximum value of the effective potential $U_\text{eff}^\text{max}$ .

A circular orbit may be either stable, or unstable. If it is unstable, a small perturbation could destabilize the orbit, but a stable orbit is more stable. To determine the stability of a circular orbit, determine the concavity of the effective potential. If the concavity is positive, the orbit is stable:

{\frac {d^{2}U_{\text{eff}}}{dr^{2}}}>0

The frequency of small oscillations, using basic Hamiltonian analysis, is

\omega = \sqrt{\frac{U_\text{eff}''}{m}}

,

where the double prime indicates the second derivative of the effective potential with respect to $r$ and it is evaluated at a minimum.

Gravitational potential

Visualisation of the effective potential in a plane containing the orbit (grey rubber-sheet model with purple contours of equal potential), the Lagrangian points (red) and a planet (blue) orbiting a star (yellow)^[1]

Consider a particle of mass m orbiting a much heavier object of mass M. Assume Newtonian mechanics, which is both classical and non-relativistic. The conservation of energy and angular momentum give two constants E and L, which have values

E = \frac{1}{2}m\left(\dot{r}^2 + r^2\dot{\phi}^2\right) - \frac{GmM}{r},

L = mr^2\dot{\phi} \,

when the motion of the larger mass is negligible. In these expressions,

\dot{r}

is the derivative of r with respect to time,

\dot{\phi}

is the angular velocity of mass m,

G is the gravitational constant,

E is the total energy, and

L is the angular momentum.

Only two variables are needed, since the motion occurs in a plane. Substituting the second expression into the first and rearranging gives

m\dot{r}^2 = 2E - \frac{L^2}{mr^2} + \frac{2GmM}{r} = 2E - \frac{1}{r^2}\left(\frac{L^2}{m} - 2GmMr\right),

\frac{1}{2}m\dot{r}^2 = E - U_\text{eff}(r),

where

U_\text{eff}(r) = \frac{L^2}{2mr^2} - \frac{GmM}{r}

is the effective potential.^{[Note 1]} The original two-variable problem has been reduced to a one-variable problem. For many applications the effective potential can be treated exactly like the potential energy of a one-dimensional system: for instance, an energy diagram using the effective potential determines turning points and locations of stable and unstable equilibria. A similar method may be used in other applications, for instance determining orbits in a general relativistic Schwarzschild metric.

Effective potentials are widely used in various condensed matter subfields, e.g. the Gauss-core potential (Likos 2002, Baeurle 2004) and the screened Coulomb potential (Likos 2001).

Notes

^ A similar derivation may be found in José & Saletan, Classical Dynamics: A Contemporary Approach, pgs. 31–33

References

^ Seidov, Zakir F. (2004). "Seidov, Roche Problem". The Astrophysical Journal. 603: 283–284. arXiv:astro-ph/0311272. Bibcode:2004ApJ...603..283S. doi:10.1086/381315.

José, JV; Saletan, EJ (1998). Classical Dynamics: A Contemporary Approach (1st ed.). Cambridge University Press. ISBN 978-0-521-63636-0..
Likos, C.N.; Rosenfeldt, S.; Dingenouts, N.; Ballauff, M.; Lindner, P.; Werner, N.; Vögtle, F.; et al. (2002). "Gaussian effective interaction between flexible dendrimers of fourth generation: a theoretical and experimental study". J. Chem. Phys. 117 (4): 1869–1877. Bibcode:2002JChPh.117.1869L. doi:10.1063/1.1486209. Archived from the original on 2011-07-19.

Baeurle, S.A.; Kroener J. (2004). "Modeling Effective Interactions of Micellar Aggregates of Ionic Surfactants with the Gauss-Core Potential". J. Math. Chem. 36 (4): 409–421. doi:10.1023/B:JOMC.0000044526.22457.bb.

Likos, C.N. (2001). "Effective interactions in soft condensed matter physics". Physics Reports. 348 (4–5): 267–439. Bibcode:2001PhR...348..267L. CiteSeerX 10.1.1.473.7668. doi:10.1016/S0370-1573(00)00141-1.

[2] A similar derivation may be found in José & Saletan, Classical Dynamics: A Contemporary Approach, pgs. 31–33

[1] Seidov, Zakir F. (2004). "Seidov, Roche Problem". The Astrophysical Journal. 603: 283–284. arXiv:astro-ph/0311272. Bibcode:2004ApJ...603..283S. doi:10.1086/381315.

[1]

[Note 1]