)
Plot of the Duffing map showing chaotic behavior, where a = 2.75 and b = 0.15.
)
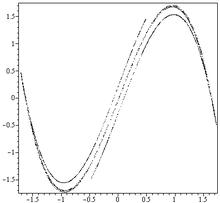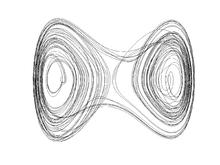
Phase portrait of a two-well Duffing oscillator (a differential equation, rather than a map) showing chaotic behavior.
The Duffing map (also called as 'Holmes map') is a discrete-time dynamical system. It is an example of a dynamical system that exhibits chaotic behavior. The Duffing map takes a point (xn, yn) in the plane and maps it to a new point given by
The map depends on the two constants a and b. These are usually set to a = 2.75 and b = 0.2 to produce chaotic behaviour. It is a discrete version of the Duffing equation.