Degree matrix

In the mathematical field of graph theory, the degree matrix is a diagonal matrix which contains information about the degree of each vertex—that is, the number of edges attached to each vertex.^[1] It is used together with the adjacency matrix to construct the Laplacian matrix of a graph.^[2]

Definition

Given a graph $G=(V,E)$ with $|V|=n$ , the degree matrix $D$ for $G$ is a $n\times n$ diagonal matrix defined as^[1]

D_{i,j}:=\left\{{\begin{matrix}\deg(v_{i})&{\mbox{if}}\ i=j\\0&{\mbox{otherwise}}\end{matrix}}\right.

where the degree $\deg(v_{i})$ of a vertex counts the number of times an edge terminates at that vertex. In an undirected graph, this means that each loop increases the degree of a vertex by two. In a directed graph, the term degree may refer either to indegree (the number of incoming edges at each vertex) or outdegree (the number of outgoing edges at each vertex).

Example

The following undirected graph has a 6x6 degree matrix with values:

Vertex labeled graph	Degree matrix
	${\begin{pmatrix}4&0&0&0&0&0\\0&3&0&0&0&0\\0&0&2&0&0&0\\0&0&0&3&0&0\\0&0&0&0&3&0\\0&0&0&0&0&1\\\end{pmatrix}}$

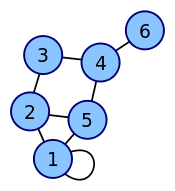Note than in the case of undirected graphs, an edge that starts and ends in the same node increases the corresponding degree value by 2 (i.e. it is counted twice).

Properties

The degree matrix of a k-regular graph has a constant diagonal of $k$ .

References

^ ^a ^b Chung, Fan; Lu, Linyuan; Vu, Van (2003), "Spectra of random graphs with given expected degrees", Proceedings of the National Academy of Sciences of the United States of America, 100 (11): 6313–6318, doi:10.1073/pnas.0937490100, MR 1982145, PMC 164443, PMID 12743375.
^ Mohar, Bojan (2004), "Graph Laplacians", in Beineke, Lowell W.; Wilson, Robin J. (eds.), Topics in algebraic graph theory, Encyclopedia of Mathematics and its Applications, 102, Cambridge University Press, Cambridge, pp. 113–136, ISBN 0-521-80197-4, MR 2125091.

[clv-1] Chung, Fan; Lu, Linyuan; Vu, Van (2003), "Spectra of random graphs with given expected degrees", Proceedings of the National Academy of Sciences of the United States of America, 100 (11): 6313–6318, doi:10.1073/pnas.0937490100, MR 1982145, PMC 164443, PMID 12743375.

[mohar-2] Mohar, Bojan (2004), "Graph Laplacians", in Beineke, Lowell W.; Wilson, Robin J. (eds.), Topics in algebraic graph theory, Encyclopedia of Mathematics and its Applications, 102, Cambridge University Press, Cambridge, pp. 113–136, ISBN 0-521-80197-4, MR 2125091.

[1]

[2]