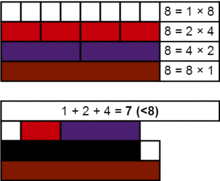
)
In number theory, a deficient number or defective number is a number n for which the sum of divisors of ‘’n’’ is less than 2n. Equivalently, it is a number for which the sum of proper divisors (or aliquot sum) is less than n. For example, the proper divisors of 8 are 1, 2, and 4, and their sum is less than 8, so 8 is deficient.
Denoting by σ(n) the sum of divisors, the value 2n − σ(n) is called the number's deficiency. In terms of the aliquot sum s(n), the deficiency is n − s(n).
Examples
The first few deficient numbers are
- 1, 2, 3, 4, 5, 7, 8, 9, 10, 11, 13, 14, 15, 16, 17, 19, 21, 22, 23, 25, 26, 27, 29, 31, 32, 33, 34, 35, 37, 38, 39, 41, 43, 44, 45, 46, 47, 49, 50, ... (sequence A005100 in the OEIS)
As an example, consider the number 21. Its proper divisors are 1, 3 and 7, and their sum is 11. Because 11 is less than 21, the number 21 is deficient. Its deficiency is 2 × 21 − 32 = 10.
Properties
Since the aliquot sums of prime numbers equal 1, all prime numbers are deficient. More generally, all odd numbers with one or two distinct prime factors are deficient. It follows that there are infinitely many odd deficient numbers. There are also an infinite number even deficient numbers.
All proper divisors of deficient numbers are deficient. Moreover, all proper divisors of perfect numbers are deficient.
There exists at least one deficient number in the interval for all sufficiently large n.[1]
![[n, n + (\log n)^2]](http://img.tfd.com/wiki/math/aa/30e4c49e65391a126244afffa7a3544a359cdfec.svg)
Related concepts
)
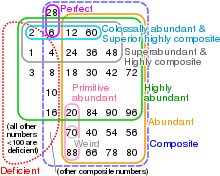
Closely related to deficient numbers are perfect numbers with σ(n) = 2n, and abundant numbers with σ(n) > 2n. The natural numbers were first classified as either deficient, perfect or abundant by Nicomachus in his Introductio Arithmetica (circa 100 CE).
See also
References
- ^ Sándor et al (2006) p.108
- Sándor, József; Mitrinović, Dragoslav S.; Crstici, Borislav, eds. (2006). Handbook of number theory I. Dordrecht: Springer-Verlag. ISBN 1-4020-4215-9. Zbl 1151.11300.