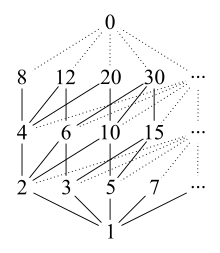
In mathematics, any two elements x and y of a set P that is partially ordered by a binary relation ≤ are comparable when either x ≤ y or y ≤ x. If it is not the case that x and y are comparable, then they are called incomparable.
A totally ordered set is exactly a partially ordered set in which every pair of elements is comparable.
It follows immediately from the definitions of comparability and incomparability that both relations are symmetric, that is x is comparable to y if and only if y is comparable to x, and likewise for incomparability.
Notation
Comparability is sometimes denoted by the symbol , and incomparability by the symbol .[1] Thus, for any pair of elements x and y of a partially ordered set, exactly one of and is true.
Comparability graphs
The comparability graph of a partially ordered set P has as vertices the elements of P and has as edges precisely those pairs {x, y} of elements for which .[2]
Classification
When classifying mathematical objects (e.g., topological spaces), two criteria are said to be comparable when the objects that obey one criterion constitute a subset of the objects that obey the other, which is to say when they are comparable under the partial order ⊂. For example, the T1 and T2 criteria are comparable, while the T1 and sobriety criteria are not.
See also
- Strict weak ordering, a partial ordering in which incomparability is a transitive relation
References
"PlanetMath: partial order". Retrieved 6 April 2010.
- ^ Trotter, William T. (1992), Combinatorics and Partially Ordered Sets:Dimension Theory, Johns Hopkins Univ. Press, p. 3
- ^ Gilmore, P. C.; Hoffman, A. J. (1964), "A characterization of comparability graphs and of interval graphs", Canadian Journal of Mathematics, 16: 539–548, doi:10.4153/CJM-1964-055-5.