Probabilistic metric space

In mathematics, probabilistic metric spaces is a generalizations of metric spaces where the distance no longer takes values in the non-negative real numbersc R_{≥ 0}, but in distribution functions.

Let D+ be the set of all probability distribution functions F such that F(0) = 0 (F is a nondecreasing, left continuous mapping from R into [0, 1] such that max(F) = 1).

Then given a non-empty set S and a function F: S × S → D+ where we denote F(p, q) by F_p,q for every (p, q) ∈ S × S, the ordered pair (S, F) is said to be a probabilistic metric space if:

For all u and v in S, u = v if and only if F_u,v(x) = 1 for all x > 0.
For all u and v in S, F_u,v = F_v,u.
For all u, v and w in S, F_u,v(x) = 1 and F_v,w(y) = 1 ⇒ F_u,w(x + y) = 1 for x, y > 0.

Probability metric of random variables

A probability metric D between two random variables X and Y may be defined, for example, as

D(X,Y)=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }|x-y|F(x,y)\,dxdy

where F(x, y) denotes the joint probability density function of the random variables X and Y. If X and Y are independent from each other then the equation above transforms into

D(X,Y)=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }|x-y|f(x)g(y)\,dxdy

where f(x) and g(y) are probability density functions of X and Y respectively.

One may easily show that such probability metrics do not satisfy the first metric axiom or satisfies it if, and only if, both of arguments X and Y are certain events described by Dirac delta density probability distribution functions. In this case:

D(X,Y)=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }|x-y|\delta (x-\mu _{x})\delta (y-\mu _{y})\,dxdy=|\mu _{x}-\mu _{y}|

the probability metric simply transforms into the metric between expected values $\mu _{x}$ , $\mu _{y}$ of the variables X and Y.

For all other random variables X, Y the probability metric does not satisfy the identity of indiscernibles condition required to be satisfied by the metric of the metric space, that is:

D\left(X,X\right)>0.

Probability metric between two random variables X and Y, both having normal distributions and the same standard deviation

\sigma = 0, \sigma = 0.2, \sigma = 0.4, \sigma = 0.6, \sigma = 0.8, \sigma = 1

(beginning with the bottom curve).

m_{xy} = |\mu_x-\mu_y|

denotes a distance between means of X and Y.

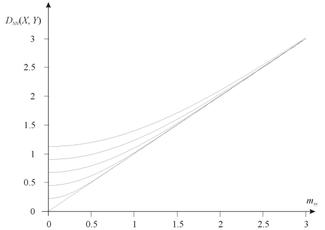
Example

For example if both probability distribution functions of random variables X and Y are normal distributions (N) having the same standard deviation $\sigma$ , integrating $D\left(X,Y\right)$ yields:

D_{NN}(X,Y)=\mu _{xy}+{\frac {2\sigma }{\sqrt {\pi }}}\operatorname {exp} \left(-{\frac {\mu _{xy}^{2}}{4\sigma ^{2}}}\right)-\mu _{xy}\operatorname {erfc} \left({\frac {\mu _{xy}}{2\sigma }}\right)

where

\mu _{xy}=\left|\mu _{x}-\mu _{y}\right|

,

and $\operatorname {erfc} (x)$ is the complementary error function.

In this case:

\lim_{\mu_{xy}\to 0} D_{NN}(X, Y) = D_{NN}(X, X) = \frac{2\sigma}{\sqrt\pi}.

Probability metric of random vectors

The probability metric of random variables may be extended into metric D(X, Y) of random vectors X, Y by substituting $|x-y|$ with any metric operator d(x, y):

D(\mathbf {X} ,\mathbf {Y} )=\int _{\Omega }\int _{\Omega }d(\mathbf {x} ,\mathbf {y} )F(\mathbf {x} ,\mathbf {y} )\,d\Omega _{x}d\Omega _{y}

where F(X, Y) is the joint probability density function of random vectors X and Y. For example substituting d(x, y) with Euclidean metric and providing the vectors X and Y are mutually independent would yield to:

D(\mathbf {X} ,\mathbf {Y} )=\int _{\Omega }\int _{\Omega }{\sqrt {\sum _{i}|x_{i}-y_{i}|^{2}}}F(\mathbf {x} )G(\mathbf {y} )\,d\Omega _{x}d\Omega _{y}.