One-sided limit

The function f(x) = x² + sign(x) has a left limit of -1, a right limit of +1, and a function value of 0 at the point x = 0.

In calculus, a one-sided limit is either of the two limits of a function f(x) of a real variable x as x approaches a specified point either from the left or from the right.

The limit as x decreases in value approaching a (x approaches a "from the right" or "from above") can be denoted:

\lim _{x\to a^{+}}f(x)\

or

\lim _{x\,\downarrow \,a}\,f(x)

or

\lim _{x\searrow a}\,f(x)

or

\lim _{x{\underset {>}{\to }}a}f(x)

The limit as x increases in value approaching a (x approaches a "from the left" or "from below") can be denoted:

\lim _{x\to a^{-}}f(x)\

or

\lim _{x\,\uparrow \,a}\,f(x)

or

\lim _{x\nearrow a}\,f(x)

or

\lim _{x{\underset {<}{\to }}a}f(x)

In probability theory it is common to use the short notation:

f(x-)

for the left limit and

f(x+)

for the right limit.

The two one-sided limits exist and are equal if the limit of f(x) as x approaches a exists. In some cases in which the limit

\lim _{x\to a}f(x)\,

does not exist, the two one-sided limits nonetheless exist. Consequently, the limit as x approaches a is sometimes called a "two-sided limit".

In some cases one of the two one-sided limits exists and the other does not, and in some cases neither exists.

The right-sided limit can be rigorously defined as

\forall \varepsilon >0\;\exists \delta >0\;\forall x\in I\;(0<x-a<\delta \Rightarrow |f(x)-L|<\varepsilon ),

and the left-sided limit can be rigorously defined as

\forall \varepsilon >0\;\exists \delta >0\;\forall x\in I\;(0<a-x<\delta \Rightarrow |f(x)-L|<\varepsilon ),

where $I$ represents some interval that is within the domain of $f$ .

Examples

Plot of the function

1/(1+2^{-1/x})

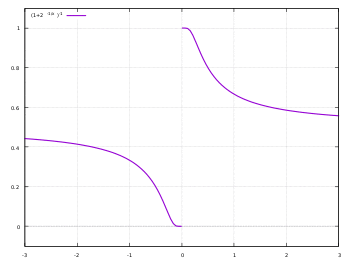
One example of a function with different one-sided limits is the following (cf. picture):

\lim _{x\to 0^{+}}{1 \over 1+2^{-1/x}}=1,

whereas

\lim _{x\to 0^{-}}{1 \over 1+2^{-1/x}}=0.

Relation to topological definition of limit

The one-sided limit to a point p corresponds to the general definition of limit, with the domain of the function restricted to one side, by either allowing that the function domain is a subset of the topological space, or by considering a one-sided subspace, including p. Alternatively, one may consider the domain with a half-open interval topology.

Abel's theorem

A noteworthy theorem treating one-sided limits of certain power series at the boundaries of their intervals of convergence is Abel's theorem.

External links

"One-sided limit". PlanetMath.

One-sided limit

Examples

Relation to topological definition of limit

Abel's theorem

See also

External links