Omnitruncation

In geometry, an omnitruncation is an operation applied to a regular polytope (or honeycomb) in a Wythoff construction that creates a maximum number of facets. It is represented in a Coxeter–Dynkin diagram with all nodes ringed.

It is a shortcut term which has a different meaning in progressively-higher-dimensional polytopes:

• Uniform polytope#Truncation operators
  • For regular polygons: An ordinary truncation, t_0,1{p} = t{p} = {2p}.
    • Coxeter-Dynkin diagram
  • For uniform polyhedra (3-polytopes): A cantitruncation, t_0,1,2{p,q} = tr{p,q}. (Application of both cantellation and truncation operations)
    • Coxeter-Dynkin diagram:
  • For Uniform 4-polytopes: A runcicantitruncation, t_0,1,2,3{p,q,r}. (Application of runcination, cantellation, and truncation operations)
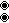
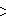
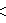
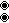
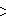
    • Coxeter-Dynkin diagram: , ,
  • For uniform polytera (5-polytopes): A steriruncicantitruncation, t_0,1,2,3,4{p,q,r,s}. (Application of sterication, runcination, cantellation, and truncation operations)
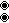
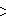
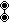
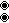
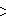
    • Coxeter-Dynkin diagram: , ,
  • For uniform n-polytopes: t_0,1,...,n-1{p₁,p₂,...,p_n}.

See also

• Expansion (geometry)
• Omnitruncated polyhedron

References

• Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8 (pp.145-154 Chapter 8: Truncation, p 210 Expansion)
• Norman Johnson Uniform Polytopes, Manuscript (1991)
  • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966

External links

• Weisstein, Eric W. "Expansion". MathWorld.

Polyhedron operators

Seed	Truncation	Rectification	Bitruncation	Dual	Expansion	Omnitruncation	Alternations
t0{p,q} {p,q}	t01{p,q} t{p,q}	t1{p,q} r{p,q}	t12{p,q} 2t{p,q}	t2{p,q} 2r{p,q}	t02{p,q} rr{p,q}	t012{p,q} tr{p,q}	ht0{p,q} h{q,p}	ht12{p,q} s{q,p}	ht012{p,q} sr{p,q}