Legendre rational functions

Plot of the Legendre rational functions for n=0,1,2 and 3 for x between 0.01 and 100.

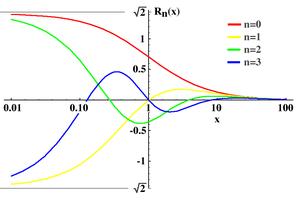
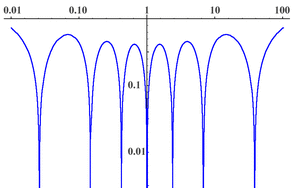
In mathematics the Legendre rational functions are a sequence of orthogonal functions on [0, ∞). They are obtained by composing the Cayley transform with Legendre polynomials.

A rational Legendre function of degree n is defined as:

R_{n}(x)={\frac {\sqrt {2}}{x+1}}\,P_{n}\left({\frac {x-1}{x+1}}\right)

where $P_n(x)$ is a Legendre polynomial. These functions are eigenfunctions of the singular Sturm-Liouville problem:

(x+1)\partial_x(x\partial_x((x+1)v(x)))+\lambda v(x)=0

with eigenvalues

\lambda_n=n(n+1)\,

Properties

Many properties can be derived from the properties of the Legendre polynomials of the first kind. Other properties are unique to the functions themselves.

Recursion

R_{n+1}(x)=\frac{2n+1}{n+1}\,\frac{x-1}{x+1}\,R_n(x)-\frac{n}{n+1}\,R_{n-1}(x)\quad\mathrm{for\,n\ge 1}

and

2(2n+1)R_n(x)=(x+1)^2(\partial_x R_{n+1}(x)-\partial_x R_{n-1}(x))+(x+1)(R_{n+1}(x)-R_{n-1}(x))

Limiting behavior

Plot of the seventh order (n=7) Legendre rational function multiplied by 1+x for x between 0.01 and 100. Note that there are n zeroes arranged symmetrically about x=1 and if x₀ is a zero, then 1/x₀ is a zero as well. These properties hold for all orders.

It can be shown that