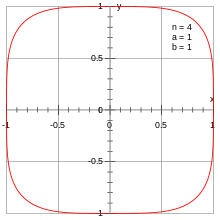
Lamé's special quartic

Lamé's special quartic with "radius" 1.

Lamé's special quartic, named after Gabriel Lamé, is the graph of the equation

x^{4}+y^{4}=r^{4}

where $r > 0$ .^[1] It looks like a rounded square with "sides" of length $2r$ and centered on the origin. This curve is a squircle centered on the origin, and it is a special case of a superellipse.^[2]

Because of Pierre de Fermat's only surviving proof, that of the n = 4 case of Fermat's Last Theorem, if r is rational there is no non-trivial rational point (x, y) on this curve (that is, no point for which both x and y are non-zero rational numbers).

References

^ Oakley, Cletus Odia (1958), Analytic Geometry Problems, College Outline Series, 108, Barnes & Noble, p. 171.
^ Schwartzman, Steven (1994), The Words of Mathematics: An Etymological Dictionary of Mathematical Terms Used in English, MAA Spectrum, Mathematical Association of America, p. 212, ISBN 9780883855119.

[1] Oakley, Cletus Odia (1958), Analytic Geometry Problems, College Outline Series, 108, Barnes & Noble, p. 171.

[2] Schwartzman, Steven (1994), The Words of Mathematics: An Etymological Dictionary of Mathematical Terms Used in English, MAA Spectrum, Mathematical Association of America, p. 212, ISBN 9780883855119.

[1]

[2]