Horseshoe lemma

In homological algebra, the horseshoe lemma, also called the simultaneous resolution theorem, is a statement relating resolutions of two objects $A'$ and $A''$ to resolutions of extensions of $A'$ by $A''$ . It says that if an object $A$ is an extension of $A'$ by $A''$ , then a resolution of $A$ can be built up inductively with the nth item in the resolution equal to the coproduct of the nth items in the resolutions of $A'$ and $A''$ . The name of the lemma comes from the shape of the diagram illustrating the lemma's hypothesis.

Formal statement

Let ${\mathcal {A}}$ be an abelian category with enough projectives. If

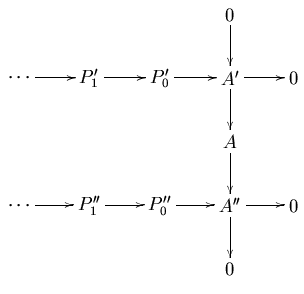
is a diagram in ${\mathcal {A}}$ such that the column is exact and the rows are projective resolutions of $A'$ and $A''$ respectively, then it can be completed to a commutative diagram

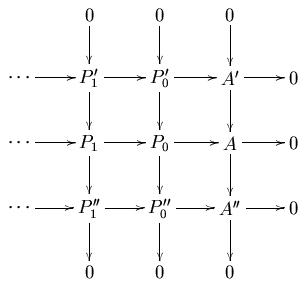
where all columns are exact, the middle row is a projective resolution of $A$ , and $P_{n}=P'_{n}\oplus P''_{n}$ for all n. If ${\mathcal {A}}$ is an abelian category with enough injectives, the dual statement also holds.

The lemma can be proved inductively. At each stage of the induction, the properties of projective objects are used to define maps in a projective resolution of $A$ . Then the snake lemma is invoked to show that the simultaneous resolution constructed so far has exact rows.

References

Henri Cartan and Samuel Eilenberg Homological algebra, Princeton University Press, 1956.
M. Scott Osborne, Basic homological algebra, Springer-Verlag, 2000.

Horseshoe lemma

Formal statement

See also

References