)
One possible binary representation of biquinary code
)
Reflected biquinary code
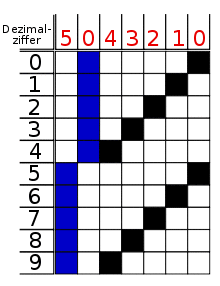
Bi-quinary coded decimal is a numeral encoding scheme used in many abacuses and in some early computers, including the Colossus.[1] The term bi-quinary indicates that the code comprises both a two-state (bi) and a five-state (quinary) component. The encoding resembles that used by many abacuses, with four beads indicating either 0 through 4 or 5 through 9 and another bead indicating which of those ranges.
Several human languages, most notably Khmer and Wolof, also use biquinary systems. For example, the Khmer word for 6, pram muoy, literally means five [plus] one. The numerals from 0 to 9 in Japanese Sign Language is based on bi-quinary, with the thumb acting as 5 units, and the rest of the fingers each standing for 1 unit. Roman numerals use a symbolic, rather than positional, bi-quinary base, even though Latin is completely decimal.
Examples
)
Copy of a Roman abacus
)
Suanpan (the number represented in the picture is 6,302,715,408)
Several different representations of bi-quinary coded decimal have been used by different machines. The two-state component is encoded as one or two bits, and the five-state component is encoded using three to five bits. Some examples are:
- Roman and Chinese abacuses
- Stibitz[2] relay calculators at Bell Labs from Model II onwards
- FACOM 128 relay calculators at Fujitsu
- IBM 650 – seven bits
- Two bi bits: 0 5 and five quinary bits: 0 1 2 3 4, with error checking.
- Exactly one bi bit and one quinary bit is set in a valid digit. In the pictures of the front panel below and in close-up, the bi-quinary encoding of the internal workings of the machine are evident in the arrangement of the lights – the bi bits form the top of a T for each digit, and the quinary bits form the vertical stem.
- (the machine was running when the photograph was taken and the active bits are visible in the close-up and just discernible in the full panel picture)
| Value | 05-01234 bits | ) ) Close-up of IBM 650 indicators |
| 0 | 10-10000 | |
| 1 | 10-01000 | |
| 2 | 10-00100 | |
| 3 | 10-00010 | |
| 4 | 10-00001 | |
| 5 | 01-10000 | |
| 6 | 01-01000 | |
| 7 | 01-00100 | |
| 8 | 01-00010 | |
| 9 | 01-00001 |
- Remington Rand 409 - five bits
- One quinary bit (tube) for each of 1, 3, 5, and 7 - only one of these would be on at the time.
- The fifth bi bit represented 9 if none of the others were on; otherwise it added 1 to the value represented by the other quinary bit.
- (sold in the two models UNIVAC 60 and UNIVAC 120)
| Value | 1357-9 bits |
| 0 | 0000-0 |
| 1 | 1000-0 |
| 2 | 1000-1 |
| 3 | 0100-0 |
| 4 | 0100-1 |
| 5 | 0010-0 |
| 6 | 0010-1 |
| 7 | 0001-0 |
| 8 | 0001-1 |
| 9 | 0000-1 |
- UNIVAC Solid State – four bits
| Value | p-5-421 bits |
| 0 | 1-0-000 |
| 1 | 0-0-001 |
| 2 | 0-0-010 |
| 3 | 1-0-011 |
| 4 | 0-0-100 |
| 5 | 0-1-000 |
| 6 | 1-1-001 |
| 7 | 1-1-010 |
| 8 | 0-1-011 |
| 9 | 1-1-100 |
- UNIVAC LARC – four bits[8]
- One bi bit: 5, three Johnson counter-coded quinary bits and one parity check bit
| Value | p-5-qqq bits |
| 0 | 1-0-000 |
| 1 | 0-0-001 |
| 2 | 1-0-011 |
| 3 | 0-0-111 |
| 4 | 1-0-110 |
| 5 | 0-1-000 |
| 6 | 1-1-001 |
| 7 | 0-1-011 |
| 8 | 1-1-111 |
| 9 | 0-1-110 |
See also
- Binary-coded decimal
- Binary number
- Chisanbop
- Finger binary
- Quinary
- Two-out-of-five code
- FACOM 128
References
- ^ "Why Use Binary? - Computerphile". YouTube. 2015-12-04. Retrieved 2020-12-10.
- ^ Stibitz, George Robert; Larrivee, Jules A. (1957). Written at Underhill, Vermont, USA. Mathematics and Computers (1 ed.). New York, USA / Toronto, Canada / London, UK: McGraw-Hill Book Company, Inc. p. 105. LCCN 56-10331. (10+228 pages)
- ^ Berger, Erich R. (1962). "1.3.3. Die Codierung von Zahlen". Written at Karlsruhe, Germany. In Steinbuch, Karl W. (ed.). Taschenbuch der Nachrichtenverarbeitung (in German) (1 ed.). Berlin / Göttingen / New York: Springer-Verlag OHG. pp. 68–75. LCCN 62-14511.
- ^ Berger, Erich R.; Händler, Wolfgang (1967) [1962]. Steinbuch, Karl W.; Wagner, Siegfried W. (eds.). Taschenbuch der Nachrichtenverarbeitung (in German) (2 ed.). Berlin, Germany: Springer-Verlag OHG. LCCN 67-21079. Title No. 1036.
- ^ Steinbuch, Karl W.; Weber, Wolfgang; Heinemann, Traute, eds. (1974) [1967]. Taschenbuch der Informatik - Band II - Struktur und Programmierung von EDV-Systemen. Taschenbuch der Nachrichtenverarbeitung (in German). 2 (3 ed.). Berlin, Germany: Springer-Verlag. ISBN 3-540-06241-6. LCCN 73-80607.
- ^ Dokter, Folkert; Steinhauer, Jürgen (1973-06-18). Digital Electronics. Philips Technical Library (PTL) / Macmillan Education (Reprint of 1st English ed.). Eindhoven, Netherlands: The Macmillan Press Ltd. / N. V. Philips' Gloeilampenfabrieken. doi:10.1007/978-1-349-01417-0. ISBN 978-1-349-01419-4. SBN 333-13360-9. Retrieved 2020-05-11. (270 pages) (NB. This is based on a translation of volume I of the two-volume German edition.)
- ^ Dokter, Folkert; Steinhauer, Jürgen (1975) [1969]. Digitale Elektronik in der Meßtechnik und Datenverarbeitung: Theoretische Grundlagen und Schaltungstechnik. Philips Fachbücher (in German). I (improved and extended 5th ed.). Hamburg, Germany: Deutsche Philips GmbH. p. 50. ISBN 3-87145-272-6. (xii+327+3 pages) (NB. The German edition of volume I was published in 1969, 1971, two editions in 1972, and 1975. Volume II was published in 1970, 1972, 1973, and 1975.)
- ^ a b Savard, John J. G. (2018) [2006]. "Decimal Representations". quadibloc. Archived from the original on 2018-07-16. Retrieved 2018-07-16.
Further reading
- Military Handbook: Encoders - Shaft Angle To Digital (PDF). United States Department of Defense. 1991-09-30. MIL-HDBK-231A. Archived (PDF) from the original on 2020-07-25. Retrieved 2020-07-25. (NB. Supersedes MIL-HDBK-231(AS) (1970-07-01).)